Machine Learning for Economists: An Introduction
Machine Learning for Economists: An Introduction
INTRODUCTION
Machine Learning (henceforth ML) refers to the set of algorithms and computational methods which enable computers to learn patterns from training data without being explicitly programmed to do so.[1] ML uses training data to learn patterns by estimating a mathematical model and making predictions in out of sample based on new or unseen input data. ML has the tremendous capacity to discover complex, flexible and crucially generalisable structure in training data. Conceptually speaking, ML can be thought of as a set of complex function approximation techniques which help us learn the unknown and potentially highly nonlinear mapping between the data and prediction outcomes, outperforming traditional techniques.[2]
In this exposition, my aim is to provide a basic and non-technical overview of machine learning and its applications for economists including development economists. For more technical and complete treatments you may consult Alpaydin (2020) and James, et al. (2013). You may also wish to refer to my four lecture series on machine learning on YouTube https:// www.youtube.com/watch?v=E9dLEAZW3L4 and my GitHub page for detailed and more technical lecture slides https://github.com/sonanmemon/Introduction-to-ML-For-Economists.
ML applications have littered the academic literature and triumphed in industry applications. A case in point is Deep Face, a deep neural network created by Facebook for facial recognition. Another poster child for ML’s success is Deep Mind’s AlphaGo program based on neural networks which defeated the world Go champion in 2016. In addition, numerous applications abound in diverse areas such as fraud detection, spam filtering, speech recognition, recommendation systems, medical diagnosis, gene prediction based on DNA sequences in genomics, sales prediction for supermarkets, customer segmentation research, stock market prediction and house price prediction.
During the past few years, economists have also harnessed the power of machine learning in their research. A few applications from recent economic literature include training neural nets on satellite data to predict local economic outcomes in African countries Jean, et al. (2016). Cellphone usage data and ML has been used to measure wealth and quantify poverty in Rwanda Blumenstock, et al. (2015), Bangladesh Steele, et al. (2017) and to identify ultra-poor households for targeting development aid better in Afghanistan Aiken, et al. (2020). Larsen, et al. (2021) used text data on news and ML to estimate the impact of news on household inflation expectations.
___________________________________
[1]ML is not identical to Artificial Intelligence (AI). It is more accurate to think of ML as a subset of AI.
[2]Using Chebyshev polynomials or manual human effort to approximate functions are examples of traditional methods.
KEY CONCEPTS IN MACHINE LEARNING
Broadly speaking, ML falls under two categories: supervised learning and unsupervised learning. Supervised learning involves training data on inputs X and output Y to learn the true mapping Y = f (X). For instance, estimating the probability of disease given patient characteristics i.e P (Y |X) requires estimating the conditional probability function. Meanwhile, unsupervised learning does not try to learn f (X) but unearths patterns and associations in the input space X without data on Y .
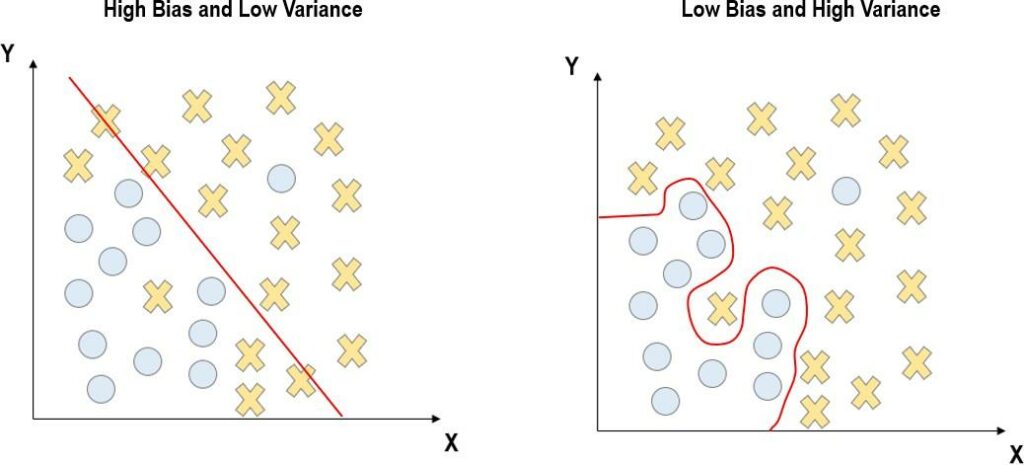
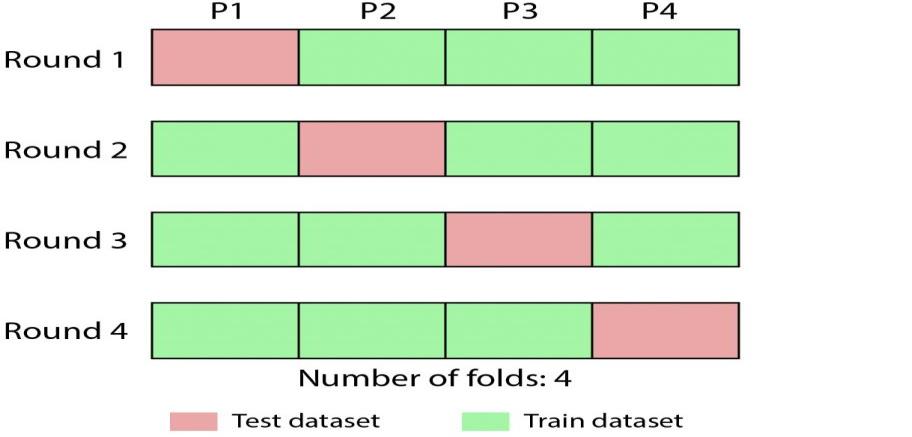
ML algorithms, when unconstrained are able to estimate an arbitrarily complex function to fit nearly any training data very accurately. However, since our goal is to make out of sample predictions and generalise, we do not want to allow the algorithm to over fit the training data. In order to prevent this over fitting problem, we tie the hands of the algorithm through regularisation, which constraints its complexity, solving the variance bias trade off. The optimal degree of regularisation is determined by what are known as tuning parameters which have to be tuned toward values that optimise out of sample prediction through cross- validation for instance. This problem is also referred to as the variance bias trade off and is illustrated in Figure 1. On the left panel, model complexity is too low, which leads to low out of sample variance but very high in-sample bias. Meanwhile, the right panel illustrates the case when there is over fitting with low in-sample bias but very high out of sample variance. Figure 2 illustrates cross-validation, a method in which we partition the data into K folds.
We hold any one fold fixed at a time and train the algorithm on the other folds but use the left out hold for prediction only. We fine tune the tuning parameters by minimising the average cross validation error, which helps us solve the variance bias trade off.
Fig. 1
For economists, it is essential to keep in mind that the coefficients in ML models do not have causal and policy relevant, structural interpretations unless we impose very strong assumptions on the data generating process. The black box which allows us to learn the true mapping Y = f (X) is still elusive and we do not yet fully understand what is going on behind the scenes. Therefore, the lesson is to look for y^ problems and not β^ problems.
Mullainathan and Spiess (2017), where prediction is the main goal and we are not interested in identification of causal parameters in the conventional econometric sense. Having said this, there is now a budding literature which leverages the power of ML to perform causal inference in experimental and observational settings (see Athey, et al. (2015).
OVERVIEW OF METHODS
There is a panoply of different methods available for economists to use, some of which are supervised learning methods for regression problems such as regularised linear regressions (e.g LASSO, elastic nets, ridge regressions), regression trees and random forests, deep learning and neural networks. Meanwhile, algorithms for supervised learning and classification problems include support vector machines and classification trees. If one is focused on unsupervised learning, then K means clustering algorithms and computational linguistics methods such as Latent Dirichlet allocation are some of the options available. In experimental settings, reinforcement learning and multi armed bandits including contextual bandits can help design treatments more optimally. For causal inference using ML, causal forests and other methods can help, especially in identifying heterogeneous treatment effects (see Athey, et al. (2015)). However, in the interest of brevity, I will provide a concise overview of only three methods: LASSO regression, multi-armed bandit problems and computational linguistics. For further understanding regarding ML in economics see Athey (2019) and Athey and Imbens (2019).
LASSO
When we are dealing with big data in the sense of large number of covariates and the goal is to make optimal predictions, it turns out that often a relatively small subset of the covariates is sufficient. In order to identify this optimal subset, we can use regularised linear regression such as Least Absolute Selection and Shrinkage Operator (LASSO).[3] Formally speaking, LASSO solves the following problem:
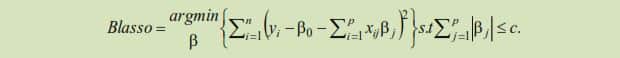 A lower level of c, which is a tuning parameter translates into more regularisation or lower complexity.
A lower level of c, which is a tuning parameter translates into more regularisation or lower complexity.
Making c sufficiently small will cause some of the coefficients to become exactly zero. The remaining set of retained non-zero coefficients are also shrunk toward zero by LASSO.
LASSO is now being frequently used in macroeconomic forecasting as well as in big scanner data for supermarkets and data in neuroeconomics. For example, Kock, et al. (2012) use a Stock and Watson type data set which has 131 macroeconomic time series for macroeconomic forecasting. LASSO throws away many of these variables in prediction problems and retains a small subset which it also shrinks toward zero, favouring sparsity of model specification.
MULTI-ARMED BANDITS
The second method that I will discuss is the multi-armed bandit problem, including contextual bandits. Traditionally, experiments were designed by assigning a predetermined number of units to each of several treatments. After outcomes are measured the average effect of the treatment would be estimated using the difference in average outcomes by treatment. This is inefficient since we waste units by assigning them to treatments that are known, albeit with a high degree of uncertainty to be inferior to some of the other treatments. Modern methods for experimentation focus on balancing exploration of new treatments[4] with exploitation of returns from treatments that are currently known to work well though these may not be the best ones.
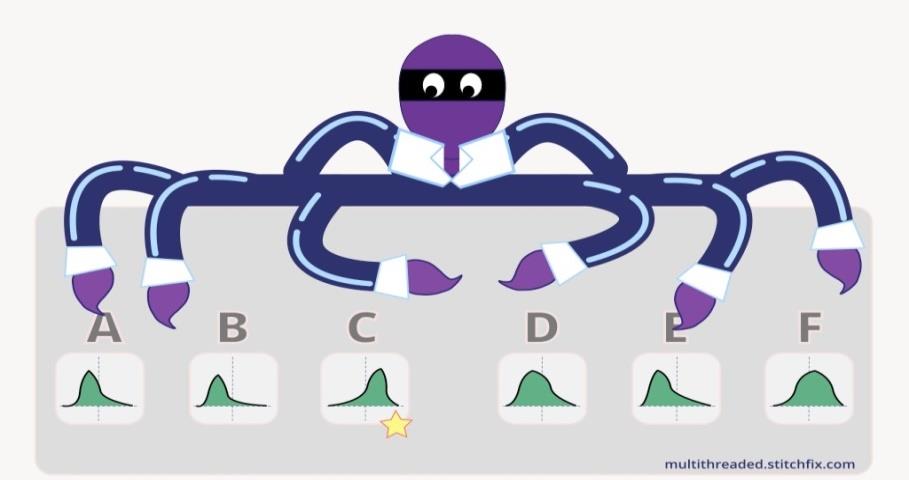
In multi-armed bandits, treatment assignment is adaptive and Bayesian, updated over time as one keeps on assigning a sequence of incoming units to various treatments. Over time, we essentially estimate the probability of each treatment being the optimal one. We re-evaluate the assignment probabilities after a batch of new observations has arrived in a Bayesian fashion. Figure 3 below depicts an octopus, which has six arms, which correspond to six treatments. Corresponding to each treatment there is a Beta distribution[5] for payoffs, which is updated over time as the octopus learns about the payoff distribution of all the treatments. As our understanding of payoff distributions improves, we allocate upcoming units to treatments with higher expected returns more often.
If all the successive units that arrive are treated as identical, then we have the standard multi-armed bandit problem. However, in experimental settings with humans, there is significant heterogeneity in units, which matters since outcome probabilities vary by unit characteristics. For instance, age, sex and genetic profile is relevant for outcome of drug trials and the probability of finding a job in response to the same labour market intervention will vary across people. When multi-armed bandit problems account for these contextual effects of treatments, they are called contextual bandits.
________________________________
[3]There are also other methods such as elastic nets and ridge regressions.
[4]This can only be done if we assign units to diverse range of treatments and explore their returns. Obviously, this involves a risk as many of the treatments may have low payoffs.
[5]The Beta distribution is used because of its flexibility and it naturally arises in the binomial case when each arm can return either success or failure.
Fig. 3.
 For instance, Caria, et al. (2021) use a version of Thompson Sampling algorithm[6] and contextual bandits for adaptive, targeted treatment assignment in a field experiment for improving job finding rate for Syrian refugees in Jordan. The algorithm balances the goal of maximising participant welfare and precision of treatment effect estimates. Caria, et al. (2021) found that after four months, cash provision has a sizable effect on employment and earnings of Syrians, while some of the other treatments such as information provision and psychological nudge were less effective.
For instance, Caria, et al. (2021) use a version of Thompson Sampling algorithm[6] and contextual bandits for adaptive, targeted treatment assignment in a field experiment for improving job finding rate for Syrian refugees in Jordan. The algorithm balances the goal of maximising participant welfare and precision of treatment effect estimates. Caria, et al. (2021) found that after four months, cash provision has a sizable effect on employment and earnings of Syrians, while some of the other treatments such as information provision and psychological nudge were less effective.
APPLICATION OF CONTEXTUAL BANDITS IN EHSAAS PROGRAM
I have currently started work on a project which aims to apply contextual, multi-armed bandit problem to improve design of treatments in the Ehsaas program, Pakistan. This program includes the BISP[7] initiative and many other health, economic and education interventions some of which include Ehsaas Kifaalat, Nashonuma, Tahafuz, Ehsaas undergraduate scholarship programs, emergency cash transfer program and many others (see https://www.pass.gov.pk/home for details).
I propose that rather than having a priori criteria for assigning a particular treatment or mix of treatments/interventions to people with certain demographic and socio-economic characteristics, one could use machine learning to learn how to optimally assign these treatments to maximise human welfare. In order to adaptively update the probability of assigning the various treatments to beneficiaries of Ehsaas, one can use algorithms which learn the mapping between individual characteristics and outcomes over time. For instance, consider that there are four possible treatments that are assigned with a priori probability of 25 percent each to a certain group of people. A contextual multi-armed bandit can adaptively learn over time which mix of treatments works best for which group of people. Once we have learned from this algorithm, we may be assigning treatment A with probability 60 percent and treatment B with probability 30 percent and the remaining two with only 5 percent probability each to a demographic group with certain features. These optimal treatment assignment probabilities which will vary by individual characteristics cannot be learned without a data driven and machine learning approach.
COMPUTATIONAL LINGUISTICS
One big contribution of ML to econometrics is that it makes new forms of data amenable to quantitative analysis: text, images, satellite data, cellphone use data etc. This brings me to my third class of methods, which include algorithms for analysing text data. One method within this class that is extremely influential and has inspired some of the best, recent work in economics on text data is topical modeling of text corpora using Latent Dirichlet Allocation. For a comprehensive survey of literature using text as data in economics see Gentzkow, et al. (2019).
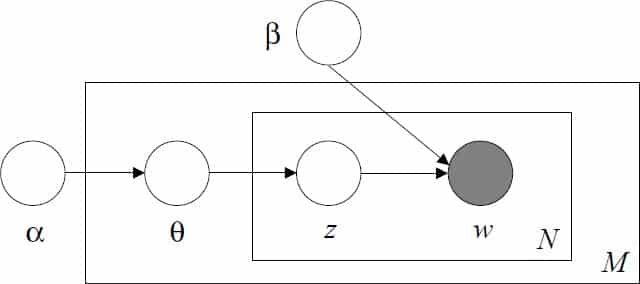
Latent Dirichlet allocation is a three-level hierarchical Bayesian model, also known as a generative probabilistic model (for technical details see Blei, et al. (2003)) for modeling collection of discrete data such as text corpora. In this literature, a document is simply a string of words and a corpus is collection of documents. A topic (z) is a probability distribution over the underlying topics. A word (w) is a probability distribution over topics. For instance, if the topic is about positive sentiment, then words which correlate with positive affect will have higher probability of being associated with this topic as opposed to other topics. LDA allows for topic probabilities to vary across documents, so that we can allow for the fact that some documents such as news articles are more optimistic than others, for instance. We can also allow for multiple topics to co-exist within the same document which allows a richer representation of the diverse information within a document.[8]
LDA first draws a parameter q for each document in the corpus from the Dirichlet distribution with hyper parameter α, which always returns values from a K−1 dimensional simplex when there are K topics. Subsequently, it draws topics for each word in the document from a multinomial distribution with parameter q. Then, it draws words from the distribution, conditional on topics. Finally, the probability of a document, which is ultimately a distribution over words can also be determined. This hierarchical Bayesian process is illustrated in the following “plate diagram” in Figure 4. The parameters in LDA are estimated using Bayesian methods.[9]
______________________________
[6]Thompson Sampling is a popular algorithm to computationally solve a multi-armed bandit problem. Upper Confidence Bound (UCB) algorithm is another option.
[7]Benazir Income Support Program.
[8]This is unlike previous methods for text analysis such as unigrams and mixture of unigram models Blei, et al. (2003).
[9]Markov Chain Monte Carlo (MCMC) methods, especially Gibbs Sampling methods are used to estimate these models. The original Blei, et al. (2003) paper also proposed an expectation maximisation algorithm which is based on variational inference.
Fig. 4.
 Source: Blei, et al. (2003).
Source: Blei, et al. (2003).
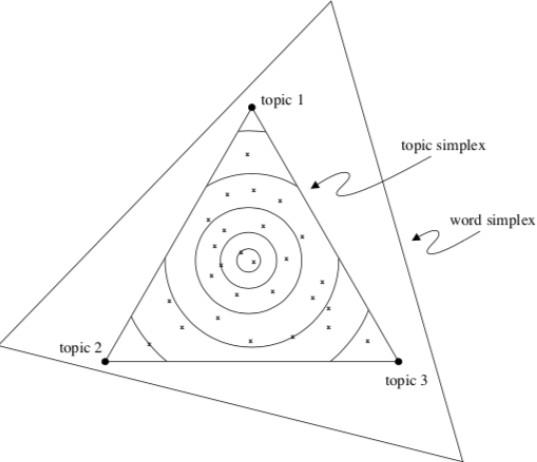
Each item or word of a document is modeled as a probability distribution over an underlying set of topics. Each topic is in turn a distribution over the underlying set of topic probabilities. This gives rise to a word simplex,[10] where each word is a probability distribution over topics and a topic simplex, which is embedded within the word simplex as shown in Figure 5 below.
Fig. 5.
 Source: Blei, et al. (2003).
Source: Blei, et al. (2003).
In the context of text modeling, the topic probabilities provide a compact representation of a document. For instance, if we choose to estimate 5 topics based on a collection of documents, LDA will identify these topics based on associations of words in the data without any supervision on what those topics are about. This can help us extract a sparse and meaningful representation from an otherwise very high dimensional text, which can be used to perform linguistic analysis and measure various tendencies in the communication and sentiment, latent in the text.
Economists have used LDA to analyse the effects of the content of central bank communication such as forward guidance and signals about the current state of the economy on market and real variables Hansen and McMahon (2016). Figure 6 shows two-word clouds, where each of the two represents the topics estimated by LDA. Words which are represented using larger fonts in these clouds have higher estimated probability of occurrence in that topic. Another shining example from cutting edge research Larsen, et al. (2021) is the use of 5 million news article archives to estimate several topics using LDA, relevant for inflation and examine the impact of these news on household inflation expectations. Larsen, et al. (2021) concluded that the topics about inflation discussed in media reporting significantly drive and predict household inflation expectations.
__________________________
[10] Note that a simplex is defined by the set of vectors for which it is true that the components sum to one.
Fig. 6.
 Source: Hansen and McMahon (2016).
Source: Hansen and McMahon (2016).
ML FOR DEVELOPMENT
There are many applications of machine learning in development economics, which can prove fruitful for policy-makers in Pakistan. For instance in Delhi, India, ML algorithms on tax data were used to more systematically identify “suspicious” firms to target for physical audits, which can improve tax compliance Mahajan and Mittal (2017). Existing data on firm characteristics for firms that were physically inspected and found to be suspicious was used to train ML algorithms, which can identify firms that should be audited, translating into improvements worth millions of dollars in tax collection for Delhi alone Mahajan and Mittal (2017).
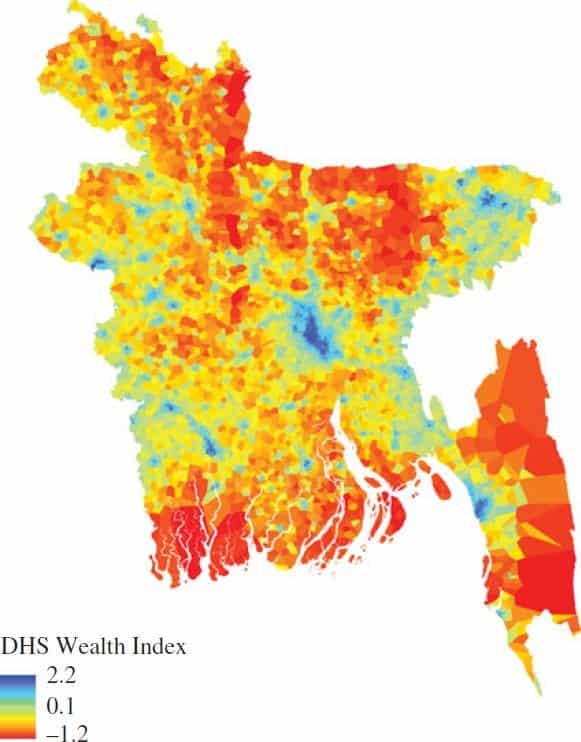
A combination of mobile CDR data (e.g. data on SMS traffic, top up patters, call durations, social network of mobile user), satellite data (e.g. vegetation indices, water bodies’ identification and urban or built area classification) and geographically referenced survey data was used by Steele, et al. (2017) to create granular poverty maps for Bangladesh. Figure 7 illustrates such a map, where the unit of analysis was based on Voronoi polygons, corresponding to cell phone tower coverage. This methodology enables prediction of poverty levels based on mobile CDR and satellite data throughout Bangladesh at fine spatial scales.
Fig. 7.
 Source: Steele, et al. (2017).
Source: Steele, et al. (2017).
Goldblatt, et al. (2018) used nighttime lights data to “train” for better classification of urban areas in daytime satellite images (Landsat) in the form of built versus non-built areas. They used nigh time luminosity data as inputs to predict the probability that a given spatial unit is a built area such as for residential or industrial or commercial purpose. Figure 8 shows a map, which identifies built urban areas in red for a region in India at a highly granular level. Non-built areas may include water bodies and vegetation. This analysis can produce more accurate data on the pace and extent of urbanisation, improving infrastructure development, industrial policy, environmental planning, and land management.
Fig. 8.
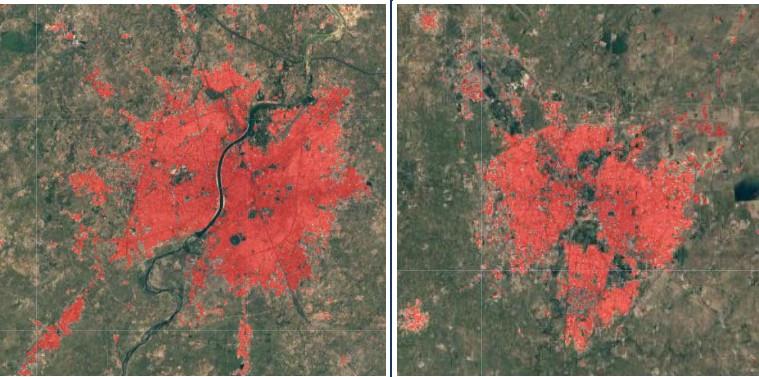 Source: Goldblatt, et al. (2018).
Source: Goldblatt, et al. (2018).
Such methodologies enable us to conduct novel and highly granular analysis, which can be updated at low cost and high frequency, addressing the challenges inherent in data scarce environments of developing countries. While it is true that ML systems for the most part and on their own cannot help us make causal inferences, but with big data, they can enhance predictions, which can automate policy decisions, identify vulnerable populations and regions as well as provide valuable inputs to causal analyses.
CONCLUSION
ML has created plethora of new opportunities for economic researchers. It is about time that we should begin to deploy big data and machine learning tools more commonly in academic research and public policy design in Pakistan. These algorithms can improve prediction, enhance the scope of causal inferences, partially compensate for deficiency of rich data by making new data sources exploitable and improve design and efficiency of various public sector programs in Pakistan. ML can help improve tax compliance, targeting of social protection, make education and health interventions in the Ehsaas program more effective, facilitate in building rich urban profiles and create rich development and security indicators across space more comprehensively among many other payoffs.
REFERENCES
Aiken, Emily L, Bedoya, Guadalupe, Coville, Aidan, & Blumenstock, Joshua E. (2020). Targeting development aid with machine learning and mobile phone data: Evidence from an anti-poverty intervention in Afghanistan. In “Proceedings of the 3rd ACM SIG- CAS Conference on Computing and Sustainable Societies” 2020, pp. 310–311.
Alpaydin, Ethem (2020). Introduction to machine learning, MIT Press.
Athey, Susan (2019). The impact of machine learning on economics. In “The economics of artificial intelligence,” University of Chicago Press, pp. 507–552.
Athey & Imbens, Guido W. (2019). Machine learning methods that economists should know about. Annual Review of Economics, 11, 685–725.
Athey, et al. (2015). Machine learning for estimating heterogeneous causal effects. (Technical Report).
Blei, David M., Ng, Andrew Y., & Jordan, Michael I. (2003). Latent dirichlet allocation. The Journal of Machine Learning Research, 3, 993–1022.
Blumenstock, Joshua, Cadamuro, Gabriel, & On, Robert (2015). Predicting poverty and wealth from mobile phone metadata. Science, 350(6264), 1073–1076.
Caria, Stefano, Kasy, Maximilian, Quinn, Simon, Shami, Soha, Teytelboym, Alex, et al. (2021). An adaptive targeted field experiment: Job search assistance for refugees in Jordan.
Gentzkow, Matthew, Kelly, Bryan, & Taddy, Matt (2019). Text as data. Journal of Economic Literature, 57 (3), 535–74.
Goldblatt, Ran, Stuhlmacher, Michelle F. & Tellman, Beth, Clinton, Nicholas, Hanson, Gordon, Georgescu, Matei, Wang, Chuyuan, Serrano-Candela, Fidel. Khandelwal, Amit K., Cheng, Wan-Hwa, et al. (2018). Using Landsat and night-time lights for supervised pixel-based image classification of urban land cover. Remote Sensing of Environment, 205, 253–275.
Hansen, Stephen, & McMahon, Michael (2016). Shocking language: Understanding the macroeconomic effects of central bank communication. Journal of International Economics, 99, S114–S133.
James, Gareth, Witten, Daniela, Hastie, Trevor, & Tibshirani, Robert (2013). An introduction to statistical learning, Vol. 112, Springer.
Jean, Neal, Burke, Marshall, Xie, Michael, Davis, W. Matthew, Lobell, David B., & Ermon, Stefano (2016). Combining satellite imagery and machine learning to predict poverty. Science, 353(6301), 790–794.
Kock, Anders Bredahl & Callot, Laurent, A. F. et al. (2012). Oracle efficient estimation and forecasting with the adaptive lasso and the adaptive group lasso in vector autoregressions. School of Economics and Management.
Larsen, Vegard H., Thorsrud, Leif Anders, & Zhulanova, Julia (2021). News-driven inflation expectations and information rigidities. Journal of Monetary Economics, 117, 507–520.
Mahajan, Aprajit, & Mittal, Shekhar (2017). Enforcement in value added tax: Is third party verification effective? (International Growth Centre Working Paper S-89412-INC-1).
Mullainathan, Sendhil & Spiess, Jann (2017). Machine learning: An applied econometric approach. Journal of Economic Perspectives, 31(2), 87–106.
Steele, Jessica E., Sundsøy, Pål Roe, Pezzulo, Carla, Alegana, Victor A., Bird, Tomas J., Blumenstock, Joshua, Bjelland, Johannes,
Engø-Monsen, Kenth, De Montjoye, Yves-Alexandre, & Iqbal, Asif M. et al. (2017). Mapping poverty using mobile phone and satellite data. Journal of The Royal Society Interface, 14(127), 20160690.